This post is a summary of the Udacity Robotics Nanodegree Lab on localization using Monte Carlo Localization (MCL). The Udacity repo can be found here

To follow this tutorial, clone the repo to a folder of your choice.

git clone https://github.com/udacity/RoboND-MCL-Lab

Monte Carlo Localization Algorithm

C++ Implementation

The following headers are used in the lab, which are mainly from the standard c++ library. One exception is the third party plotting library found here that uses python’s matplotlib as its backend.

#include "src/matplotlibcpp.h" //Graph Library
#include <iostream>
#include <string>
#include <math.h>
#include <stdexcept> // throw errors
#include <random> //C++ 11 Random Numbers
#include <vector>

namespace plt = matplotlibcpp;
using namespace std;

Next, some global variables are defined for the fixed landmarks and the world size. The random generator gets initialized and a forward declaration of two functions is made, namely mod and gen_real_random.

// Landmarks
double landmarks[8][2] = { { 20.0, 20.0 }, { 20.0, 80.0 }, { 20.0, 50.0 },
    { 50.0, 20.0 }, { 50.0, 80.0 }, { 80.0, 80.0 },
    { 80.0, 20.0 }, { 80.0, 50.0 } };

// Map size in meters
double world_size = 100.0;

// Random Generators
random_device rd;
mt19937 gen(rd());

// Global Functions
double mod(double first_term, double second_term);
double gen_real_random();

Robot Base Class

The lab uses a robot class that initializes a robot with a random x and y location and orientation in its constructor.

Robot()
{
    // Constructor
    x = gen_real_random() * world_size; // robot's x coordinate
    y = gen_real_random() * world_size; // robot's y coordinate
    orient = gen_real_random() * 2.0 * M_PI; // robot's orientation

    forward_noise = 0.0; //noise of the forward movement
    turn_noise = 0.0; //noise of the turn
    sense_noise = 0.0; //noise of the sensing
}
void set(double new_x, double new_y, double new_orient)
{
    // Set robot new position and orientation
    if (new_x < 0 || new_x >= world_size)
        throw std::invalid_argument("X coordinate out of bound");
    if (new_y < 0 || new_y >= world_size)
        throw std::invalid_argument("Y coordinate out of bound");
    if (new_orient < 0 || new_orient >= 2 * M_PI)
        throw std::invalid_argument("Orientation must be in [0..2pi]");

    x = new_x;
    y = new_y;
    orient = new_orient;
}
void set_noise(double new_forward_noise, double new_turn_noise, double new_sense_noise)
{
    // Simulate noise, often useful in particle filters
    forward_noise = new_forward_noise;
    turn_noise = new_turn_noise;
    sense_noise = new_sense_noise;
}
vector<double> sense()
{
    // Measure the distances from the robot toward the landmarks
    vector<double> z(sizeof(landmarks) / sizeof(landmarks[0]));
    double dist;
    for (int i = 0; i < sizeof(landmarks) / sizeof(landmarks[0]); i++) {
        dist = sqrt(pow((x - landmarks[i][0]), 2) + pow((y - landmarks[i][1]), 2));
        dist += gen_gauss_random(0.0, sense_noise);
        z[i] = dist;
    }
    return z;
}
Robot move(double turn, double forward)
{
    if (forward < 0)
        throw std::invalid_argument("Robot cannot move backward");

    // turn, and add randomness to the turning command
    orient = orient + turn + gen_gauss_random(0.0, turn_noise);
    orient = mod(orient, 2 * M_PI);

    // move, and add randomness to the motion command
    double dist = forward + gen_gauss_random(0.0, forward_noise);
    x = x + (cos(orient) * dist);
    y = y + (sin(orient) * dist);

    // cyclic truncate
    x = mod(x, world_size);
    y = mod(y, world_size);

    // set particle
    Robot res;
    res.set(x, y, orient);
    res.set_noise(forward_noise, turn_noise, sense_noise);

    return res;
}
string show_pose()
{
    // Returns the robot current position and orientation in a string format
    return "[x=" + to_string(x) + " y=" + to_string(y) + " orient=" + to_string(orient) + "]";
}
string read_sensors()
{
    // Returns all the distances from the robot toward the landmarks
    vector<double> z = sense();
    string readings = "[";
    for (int i = 0; i < z.size(); i++) {
        readings += to_string(z[i]) + " ";
    }
    readings[readings.size() - 1] = ']';

    return readings;
}
double measurement_prob(vector<double> measurement)
{
    // Calculates how likely a measurement should be
    double prob = 1.0;
    double dist;

    for (int i = 0; i < sizeof(landmarks) / sizeof(landmarks[0]); i++) {
        dist = sqrt(pow((x - landmarks[i][0]), 2) + pow((y - landmarks[i][1]), 2));
        prob *= gaussian(dist, sense_noise, measurement[i]);
    }

    return prob;
}

The class has the following public member variables

double x, y, orient; //robot poses
double forward_noise, turn_noise, sense_noise; //robot noises

It uses the follwoing private methods

double gen_gauss_random(double mean, double variance)
{
    // Gaussian random
    normal_distribution<double> gauss_dist(mean, variance);
    return gauss_dist(gen);
}
double gaussian(double mu, double sigma, double x)
{
    // Probability of x for 1-dim Gaussian with mean mu and var. sigma
    return exp(-(pow((mu - x), 2)) / (pow(sigma, 2)) / 2.0) / sqrt(2.0 * M_PI * (pow(sigma, 2)));
}

Global functions

Other useufl global functions

// Functions
double gen_real_random()
{
    // Generate real random between 0 and 1
    uniform_real_distribution<double> real_dist(0.0, 1.0); //Real
    return real_dist(gen);
}

double mod(double first_term, double second_term)
{
    // Compute the modulus
    return first_term - (second_term)*floor(first_term / (second_term));
}

double evaluation(Robot r, Robot p[], int n)
{
    //Calculate the mean error of the system
    double sum = 0.0;
    for (int i = 0; i < n; i++) {
        //the second part is because of world's cyclicity
        double dx = mod((p[i].x - r.x + (world_size / 2.0)), world_size) - (world_size / 2.0);
        double dy = mod((p[i].y - r.y + (world_size / 2.0)), world_size) - (world_size / 2.0);
        double err = sqrt(pow(dx, 2) + pow(dy, 2));
        sum += err;
    }
    return sum / n;
}
double max(double arr[], int n)
{
    // Identify the max element in an array
    double max = 0;
    for (int i = 0; i < n; i++) {
        if (arr[i] > max)
            max = arr[i];
    }
    return max;
}

Visualization

For visualization matplotlib is used as backend.

void visualization(int n, Robot robot, int step, Robot p[], Robot pr[])
{
    //Draw the robot, landmarks, particles and resampled particles on a graph

    //Graph Format
    plt::title("MCL, step " + to_string(step));
    plt::xlim(0, 100);
    plt::ylim(0, 100);

    //Draw particles in green
    for (int i = 0; i < n; i++) {
        plt::plot({ p[i].x }, { p[i].y }, "go");
    }

    //Draw resampled particles in yellow
    for (int i = 0; i < n; i++) {
        plt::plot({ pr[i].x }, { pr[i].y }, "yo");
    }

    //Draw landmarks in red
    for (int i = 0; i < sizeof(landmarks) / sizeof(landmarks[0]); i++) {
        plt::plot({ landmarks[i][0] }, { landmarks[i][1] }, "ro");
    }

    //Draw robot position in blue
    plt::plot({ robot.x }, { robot.y }, "bo");

    //Save the image and close the plot
    plt::save("./Images/Step" + to_string(step) + ".png");
    plt::clf();
}

Main

int main()
{
    //Practice Interfacing with Robot Class
    Robot myrobot;
    myrobot.set_noise(5.0, 0.1, 5.0);
    myrobot.set(30.0, 50.0, M_PI / 2.0);
    myrobot.move(-M_PI / 2.0, 15.0);
    //cout << myrobot.read_sensors() << endl;
    myrobot.move(-M_PI / 2.0, 10.0);
    //cout << myrobot.read_sensors() << endl;

    // Create a set of particles
    int n = 1000;
    Robot p[n];

    for (int i = 0; i < n; i++) {
        p[i].set_noise(0.05, 0.05, 5.0);
        //cout << p[i].show_pose() << endl;
    }

    //Re-initialize myrobot object and Initialize a measurment vector
    myrobot = Robot();
    vector<double> z;

    //Iterating 50 times over the set of particles
    int steps = 50;
    for (int t = 0; t < steps; t++) {

        //Move the robot and sense the environment afterwards
        myrobot = myrobot.move(0.1, 5.0);
        z = myrobot.sense();

        // Simulate a robot motion for each of these particles
        Robot p2[n];
        for (int i = 0; i < n; i++) {
            p2[i] = p[i].move(0.1, 5.0);
            p[i] = p2[i];
        }

        //Generate particle weights depending on robot's measurement
        double w[n];
        for (int i = 0; i < n; i++) {
            w[i] = p[i].measurement_prob(z);
            //cout << w[i] << endl;
        }

        //Resample the particles with a sample probability proportional to the importance weight
        Robot p3[n];
        int index = gen_real_random() * n;
        //cout << index << endl;
        double beta = 0.0;
        double mw = max(w, n);
        //cout << mw;
        for (int i = 0; i < n; i++) {
            beta += gen_real_random() * 2.0 * mw;
            while (beta > w[index]) {
                beta -= w[index];
                index = mod((index + 1), n);
            }
            p3[i] = p[index];
        }
        for (int k = 0; k < n; k++) {
            p[k] = p3[k];
            //cout << p[k].show_pose() << endl;
        }

        //Evaluate the Error
        cout << "Step = " << t << ", Evaluation = " << evaluation(myrobot, p, n) << endl;

        //####   DON'T MODIFY ANYTHING ABOVE HERE! ENTER CODE BELOW ####

        //Graph the position of the robot and the particles at each step
        visualization(n, myrobot, t, p2, p3);

    } //End of Steps loop

    return 0;
}

Compile and Run

Compile with

g++ solution.cpp -o app -std=c++11 -I/usr/include/python2.7 -lpython2.7

And finally run the program with

./app

This will output:

Step = 0, Evaluation = 4.36165
Step = 1, Evaluation = 4.13259
Step = 2, Evaluation = 3.42951
Step = 3, Evaluation = 3.2404
Step = 4, Evaluation = 2.7659
Step = 5, Evaluation = 2.48962
Step = 6, Evaluation = 2.31978
Step = 7, Evaluation = 2.24096
Step = 8, Evaluation = 2.2645
Step = 9, Evaluation = 2.16855
Step = 10, Evaluation = 2.0289
Step = 11, Evaluation = 1.90762
Step = 12, Evaluation = 1.90886
Step = 13, Evaluation = 1.86255
Step = 14, Evaluation = 1.80935
Step = 15, Evaluation = 1.75033
Step = 16, Evaluation = 1.73623
Step = 17, Evaluation = 1.66427
Step = 18, Evaluation = 1.65443
Step = 19, Evaluation = 1.68175
Step = 20, Evaluation = 1.62883
Step = 21, Evaluation = 1.61669
Step = 22, Evaluation = 1.60328
Step = 23, Evaluation = 1.55554
Step = 24, Evaluation = 1.54531
Step = 25, Evaluation = 1.48853
Step = 26, Evaluation = 1.52531
Step = 27, Evaluation = 1.54713
Step = 28, Evaluation = 1.57839
Step = 29, Evaluation = 1.59364
Step = 30, Evaluation = 1.65056
Step = 31, Evaluation = 1.6718
Step = 32, Evaluation = 1.67659
Step = 33, Evaluation = 1.61774
Step = 34, Evaluation = 1.57891
Step = 35, Evaluation = 1.50999
Step = 36, Evaluation = 1.40922
Step = 37, Evaluation = 1.40538
Step = 38, Evaluation = 1.41737
Step = 39, Evaluation = 1.39369
Step = 40, Evaluation = 1.38676
Step = 41, Evaluation = 1.43119
Step = 42, Evaluation = 1.39935
Step = 43, Evaluation = 1.37321
Step = 44, Evaluation = 1.4212
Step = 45, Evaluation = 1.55304
Step = 46, Evaluation = 1.75291
Step = 47, Evaluation = 1.93479
Step = 48, Evaluation = 1.94307
Step = 49, Evaluation = 1.25727

Results

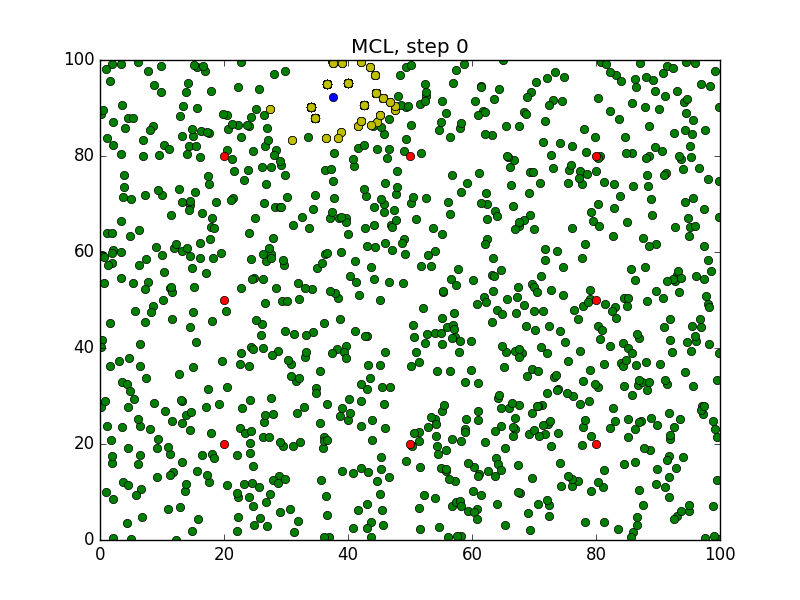
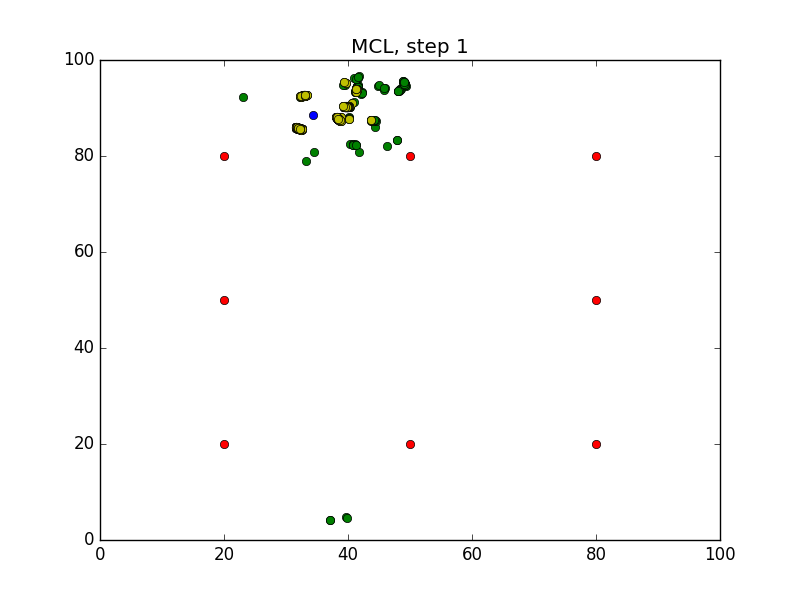
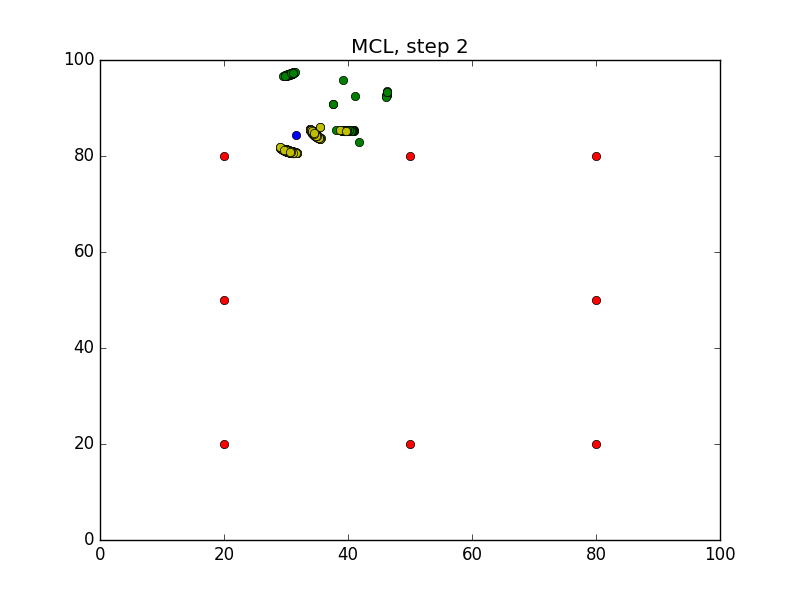
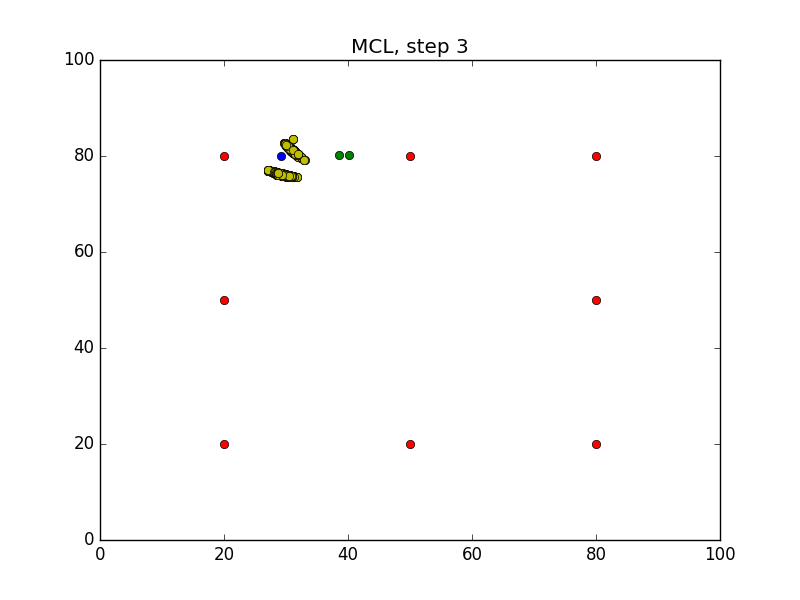
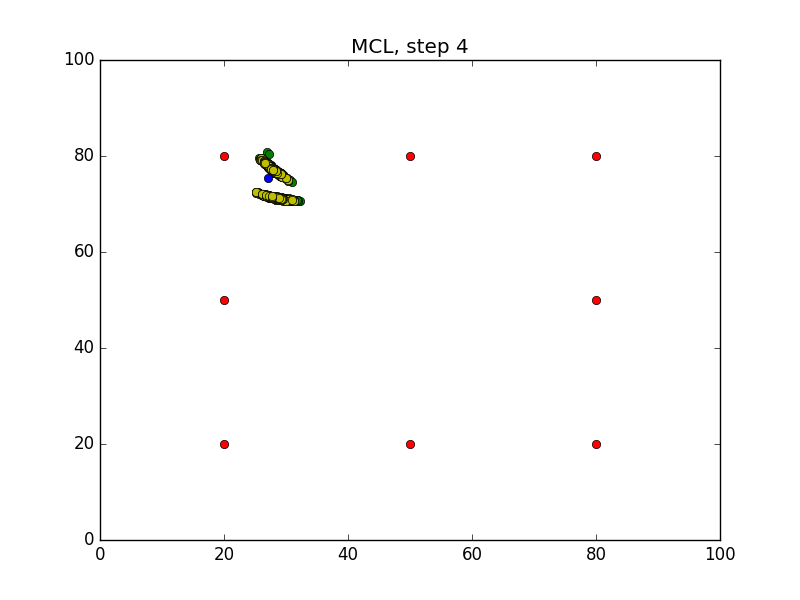
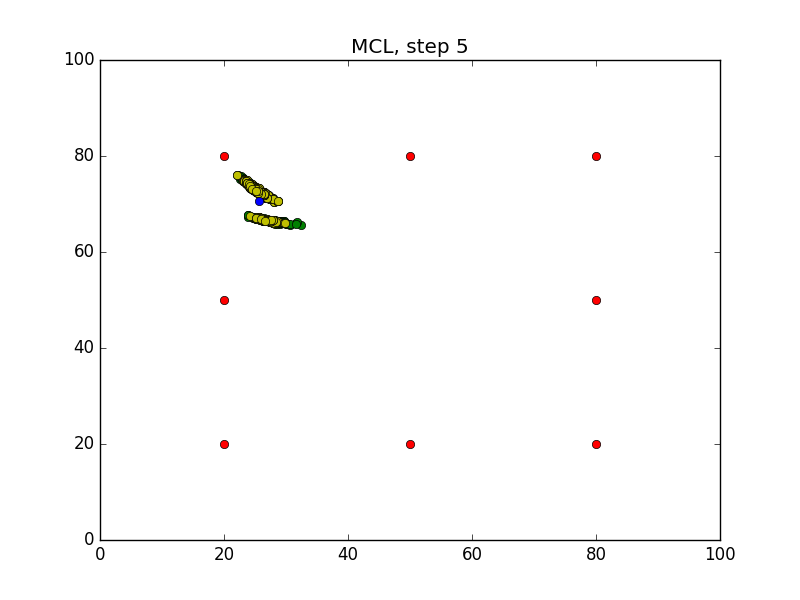
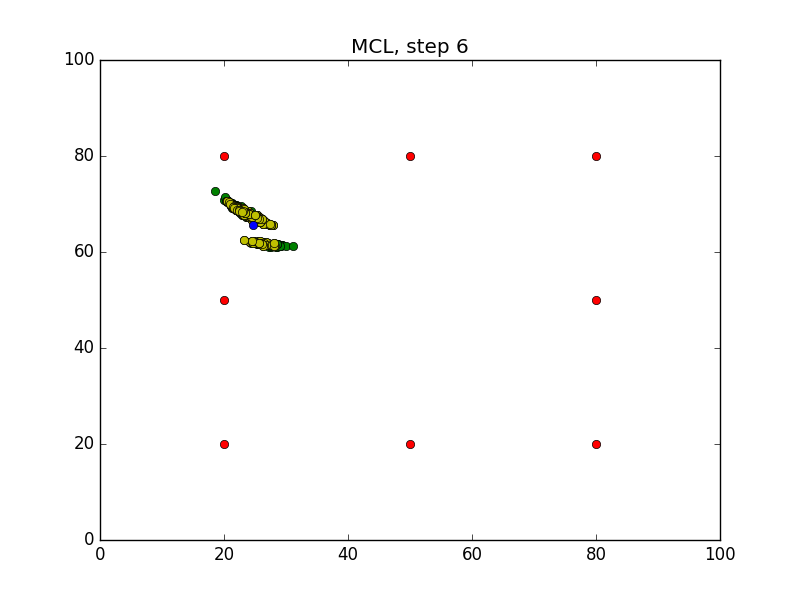
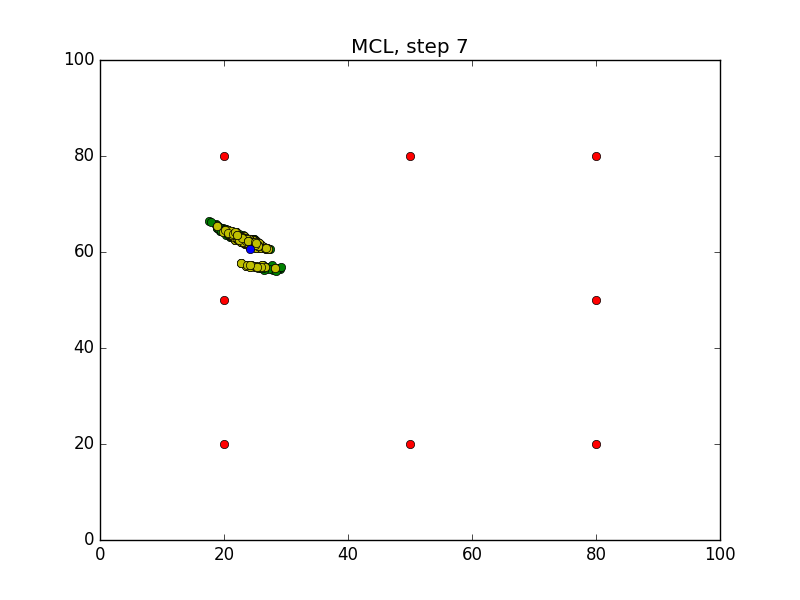
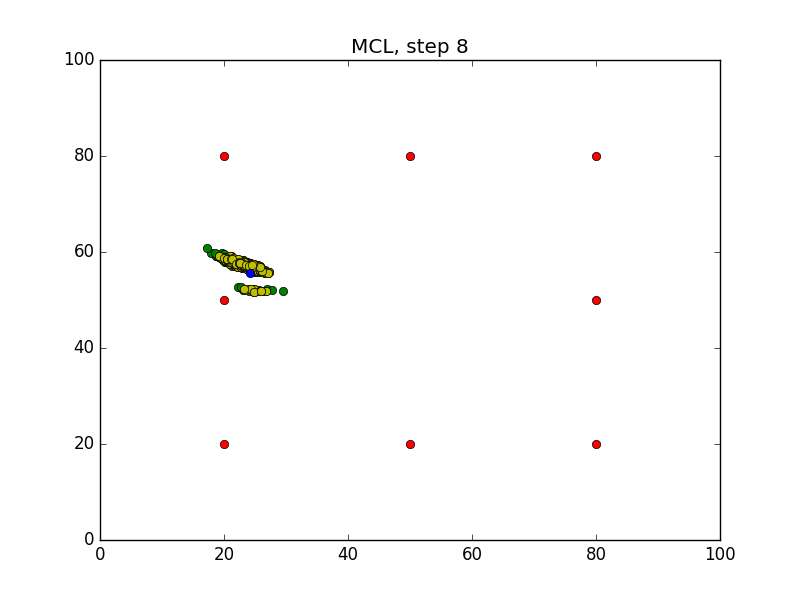
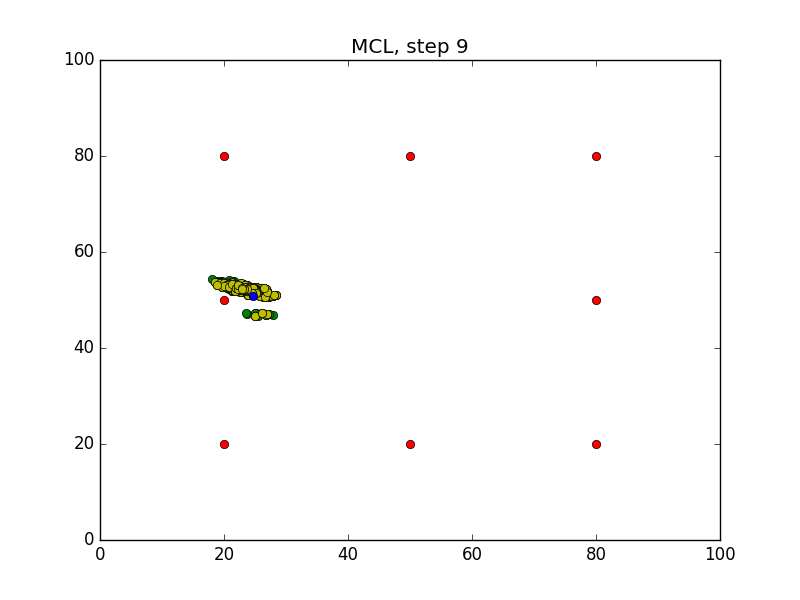
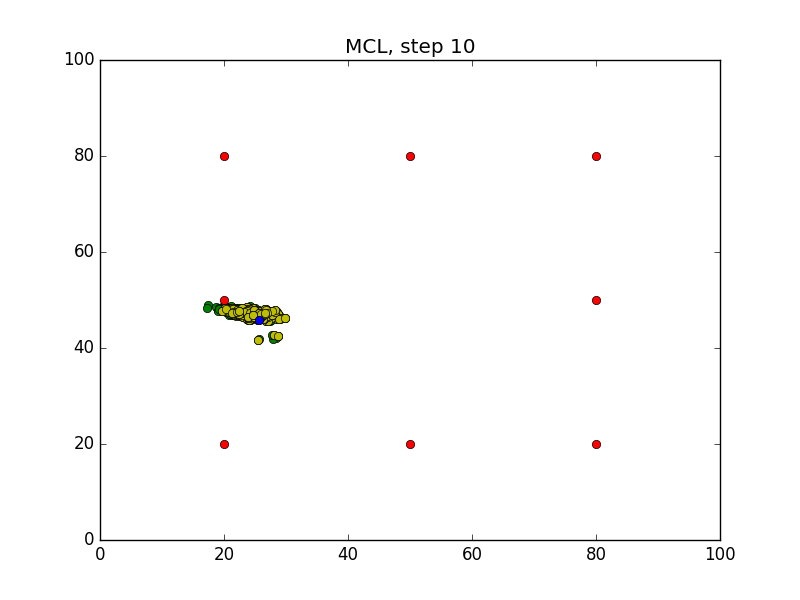
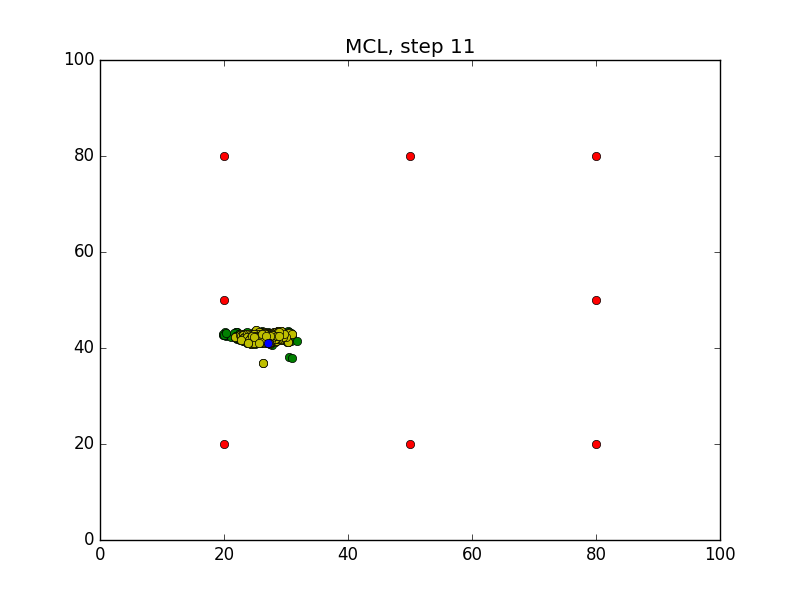
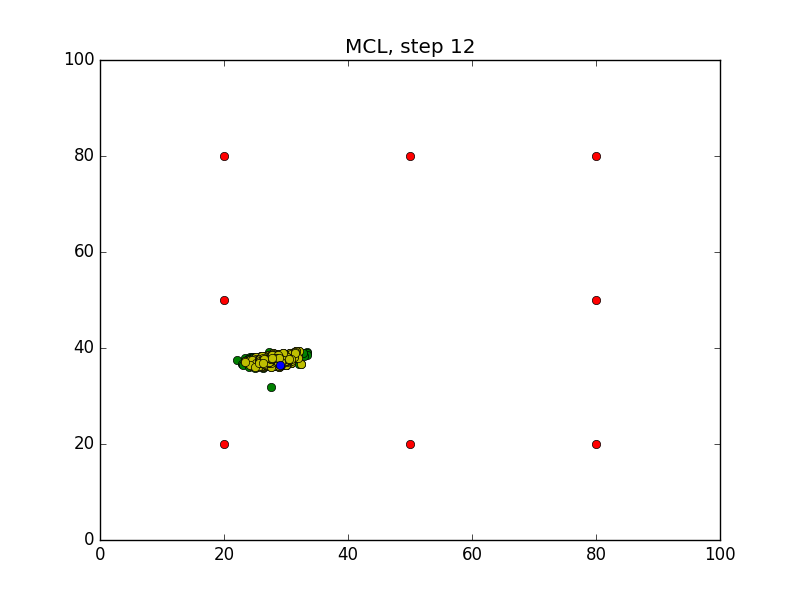
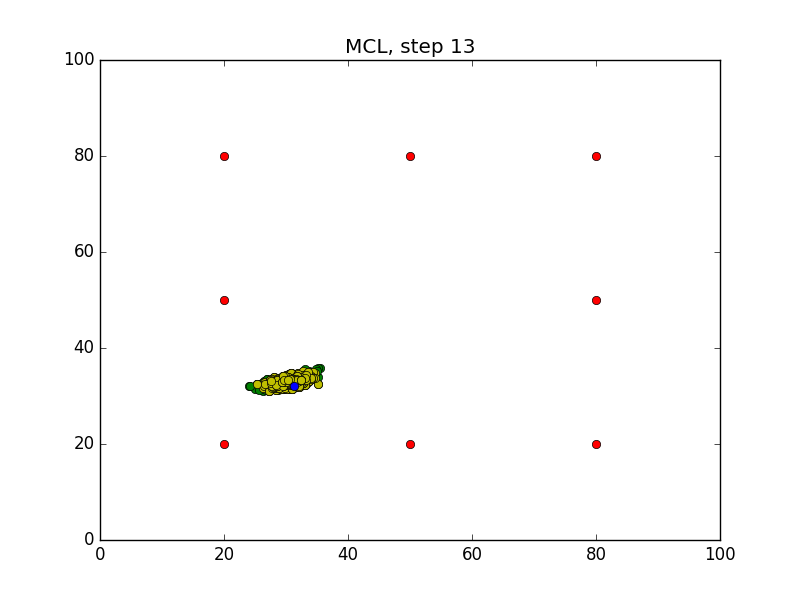
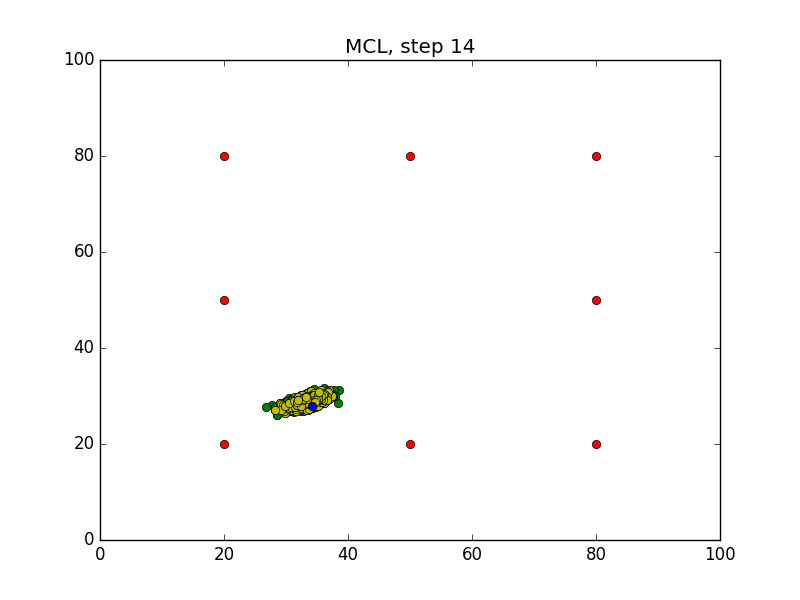
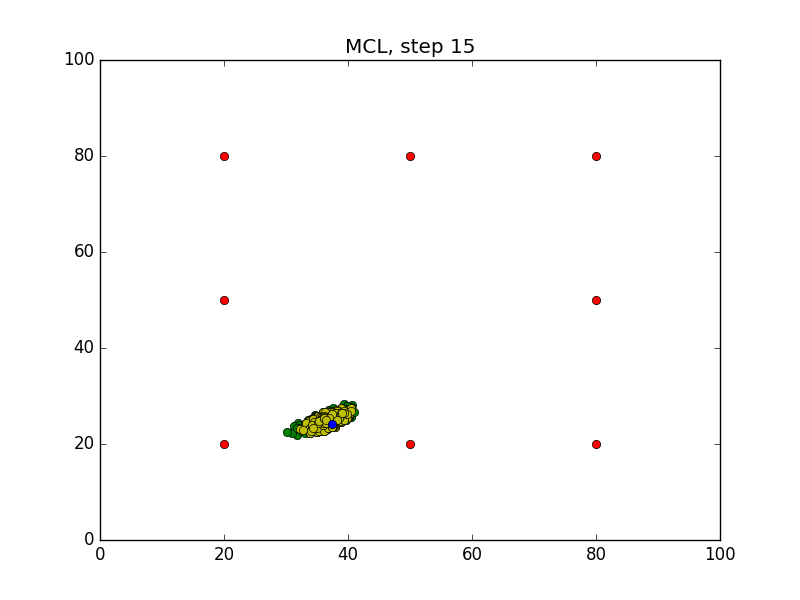
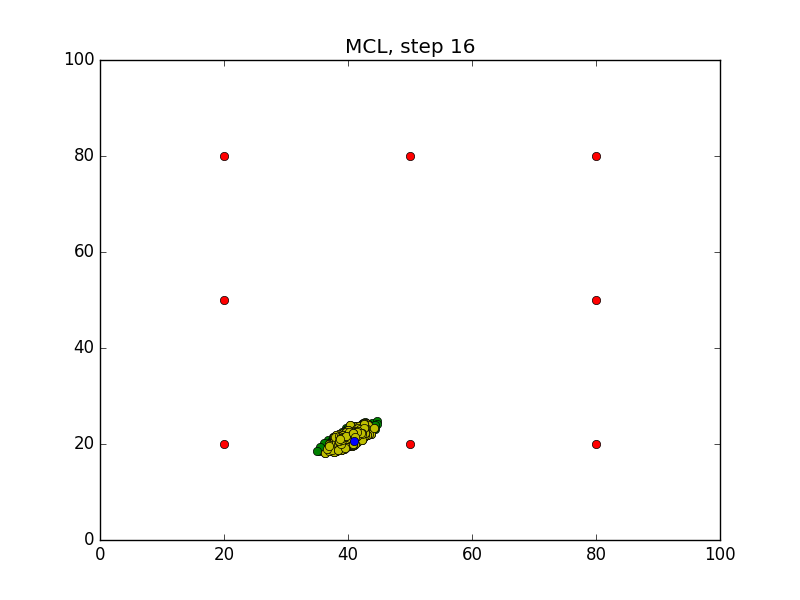
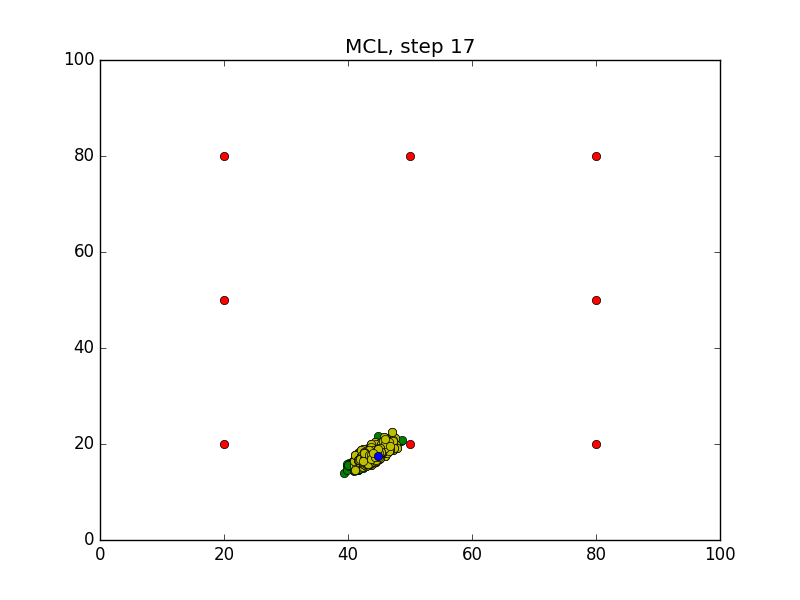
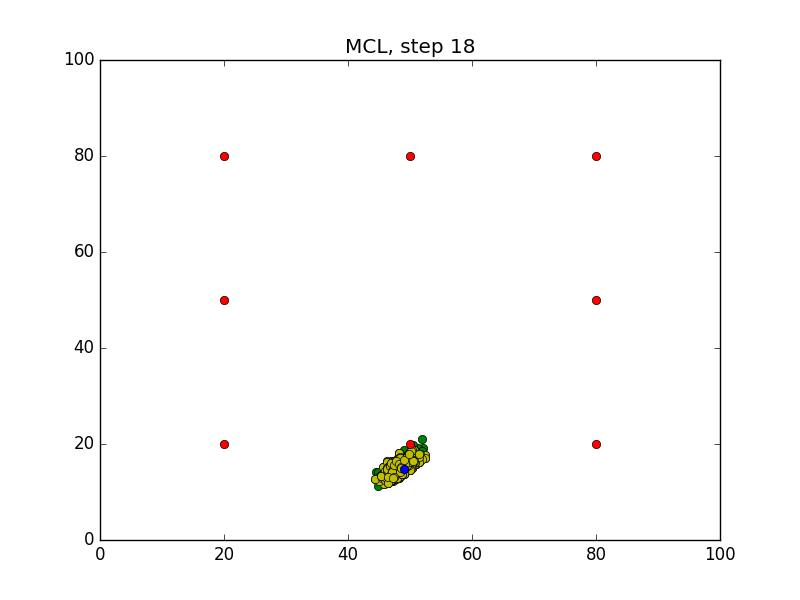
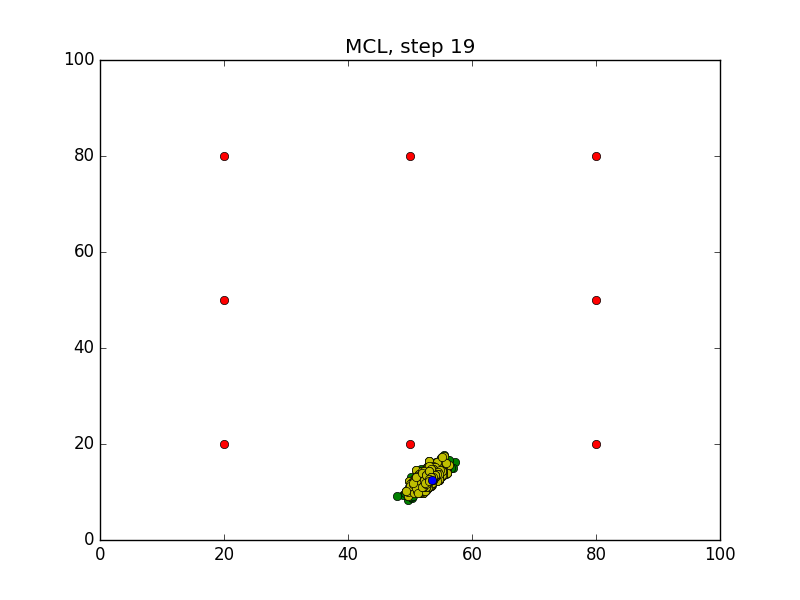
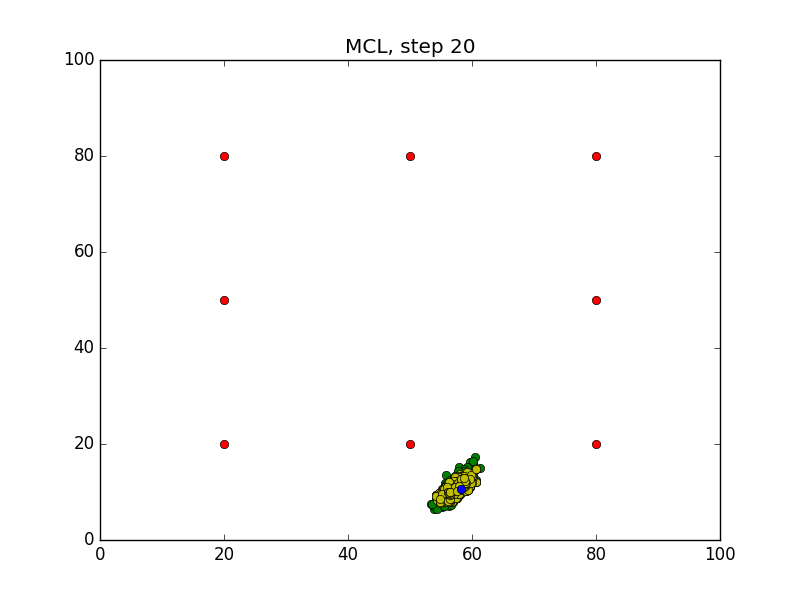
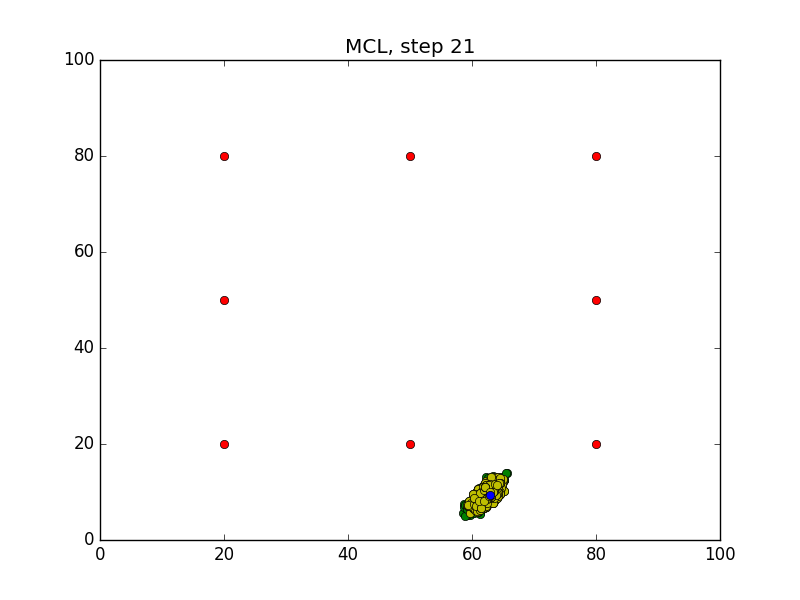
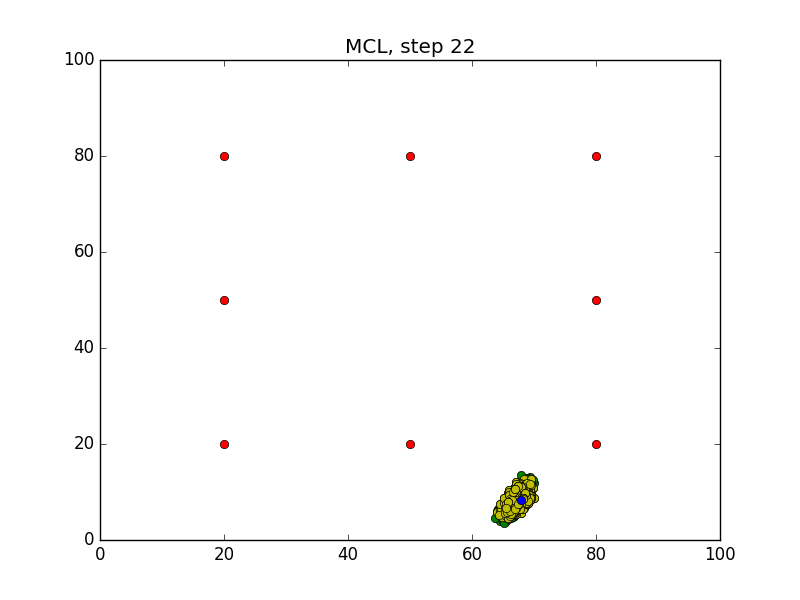
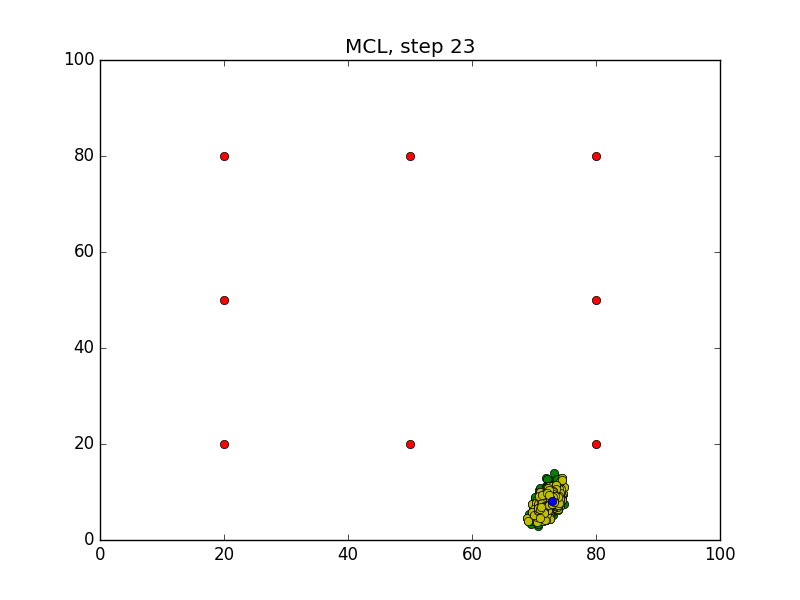
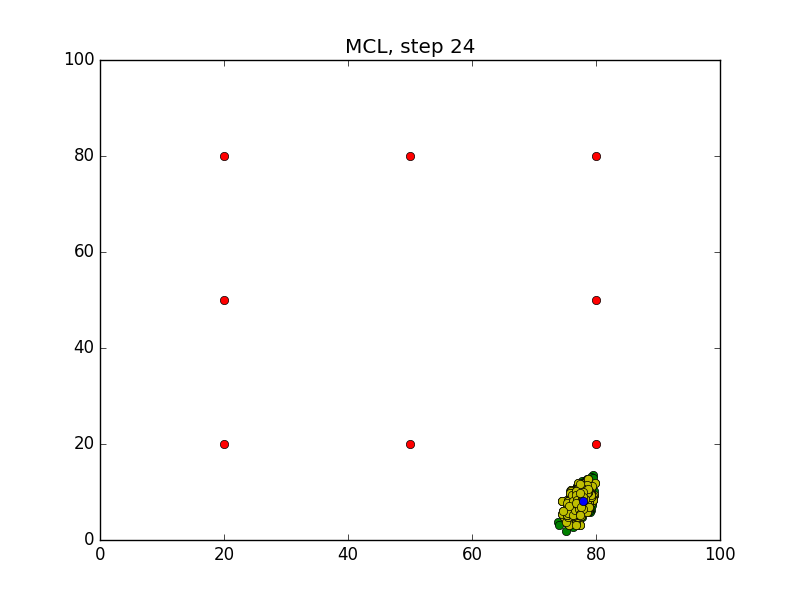
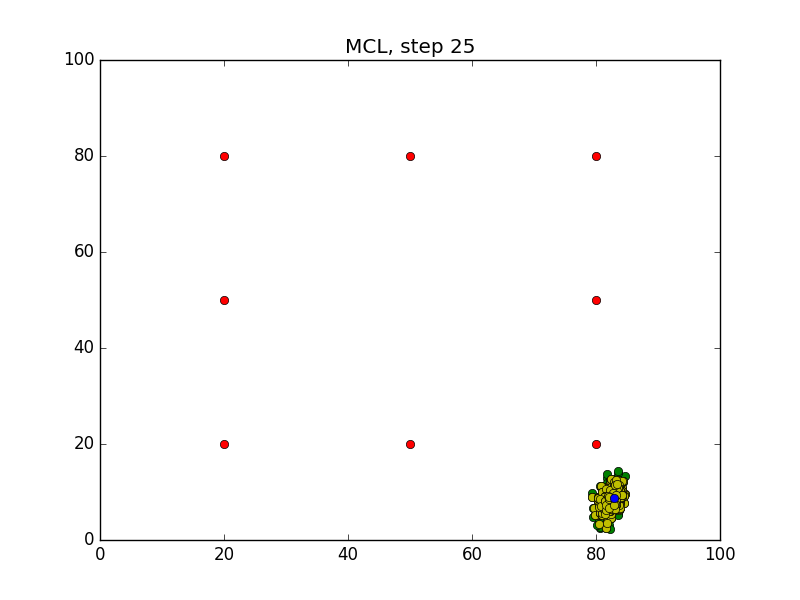
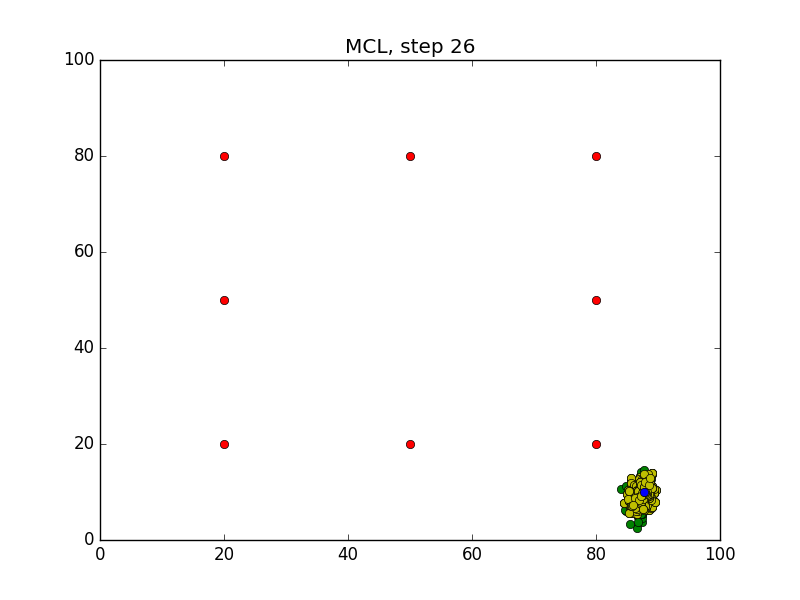
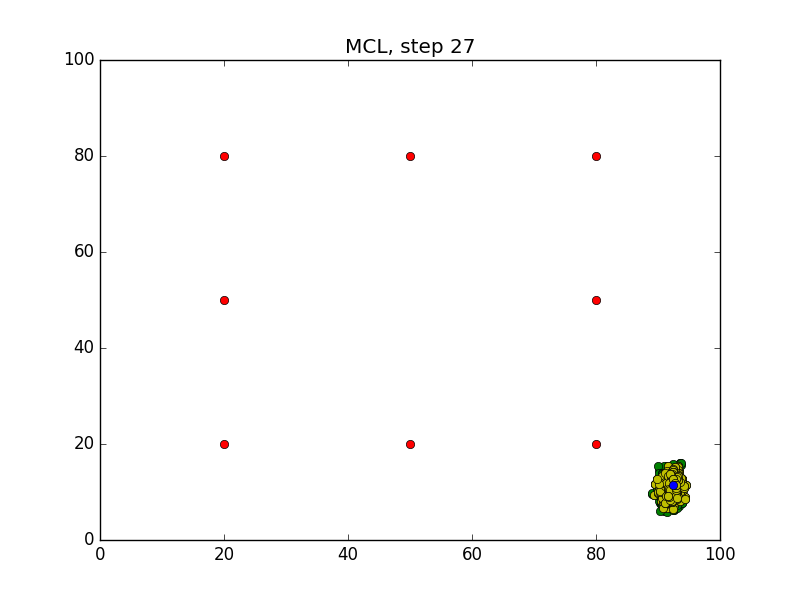
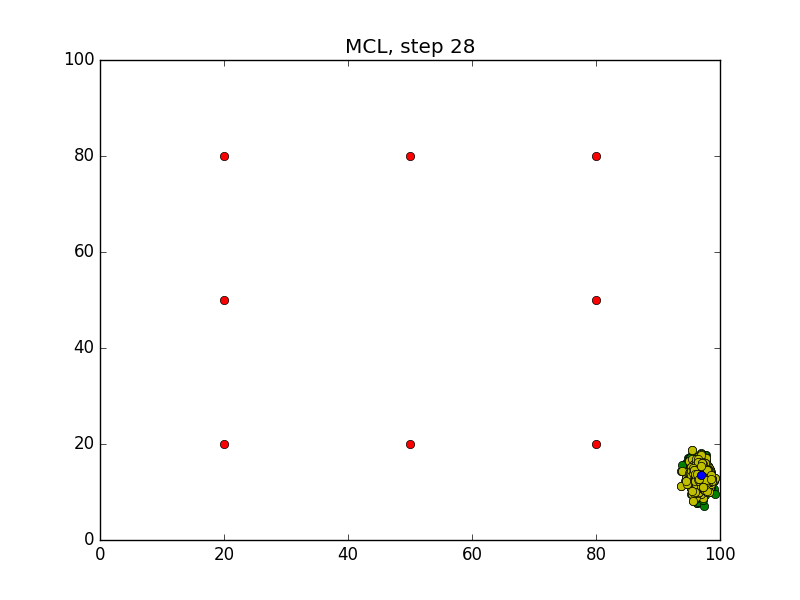
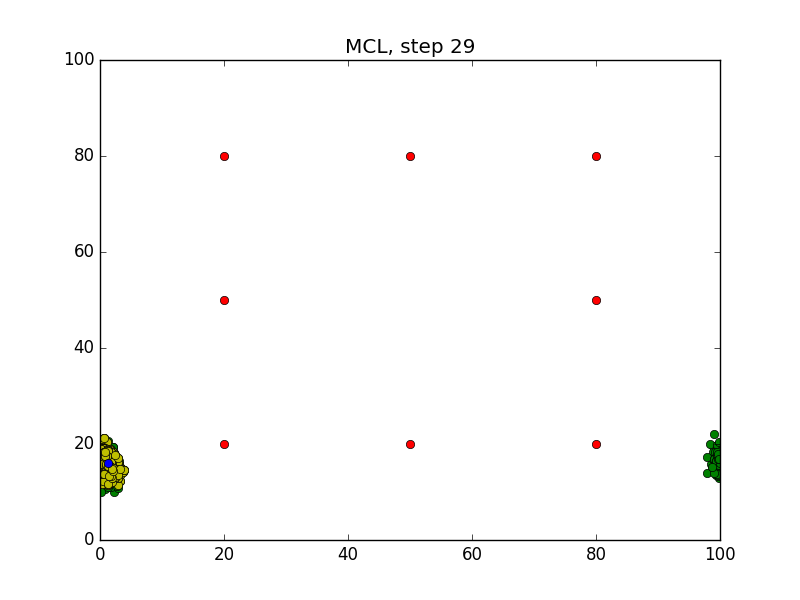
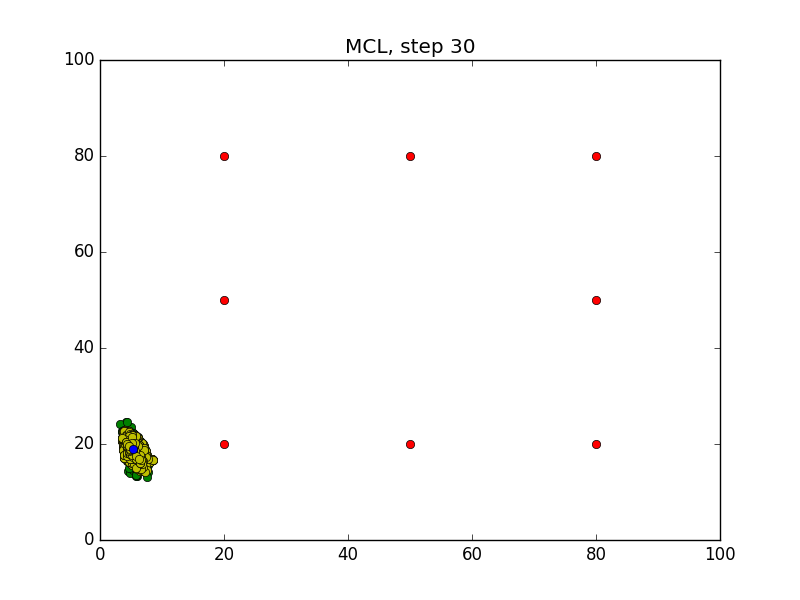
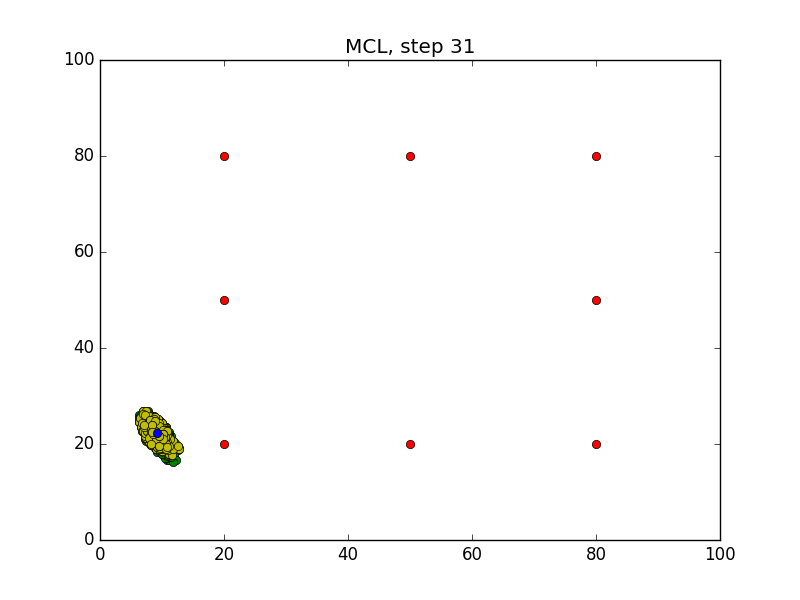
Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Iteration 10 Iteration 11 Iteration 12 Iteration 13 Iteration 14 Iteration 15 Iteration 16 Iteration 17 Iteration 18 Iteration 19 Iteration 20 Iteration 21 Iteration 22 Iteration 23 Iteration 24 Iteration 25 Iteration 26 Iteration 27 Iteration 28 Iteration 29 Iteration 30 Iteration 31 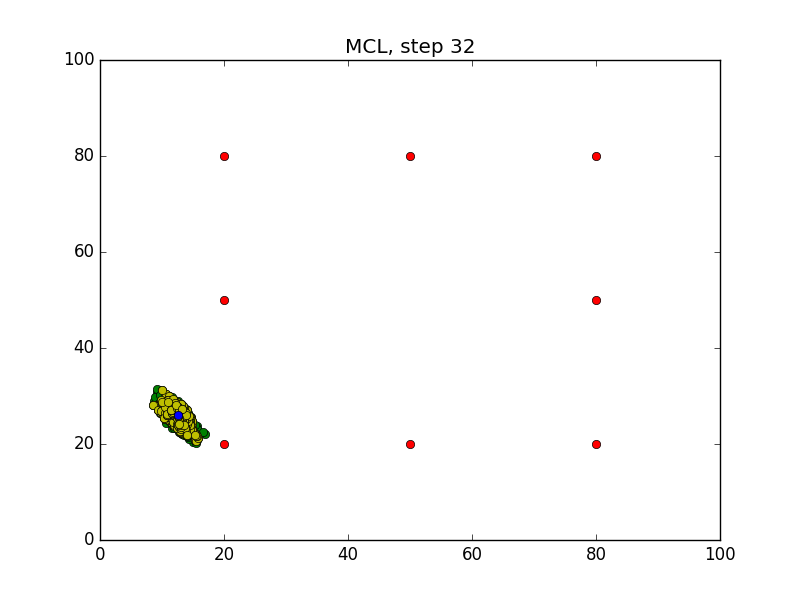Iteration 32 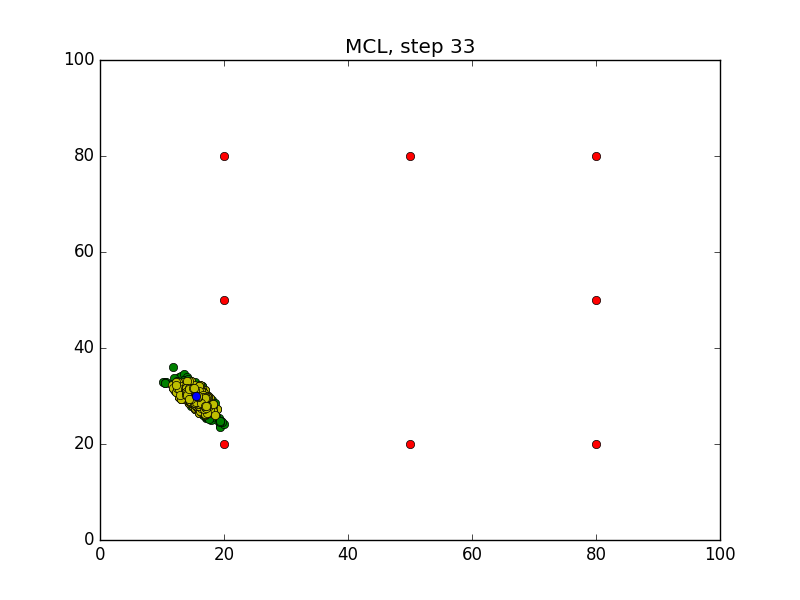Iteration 33 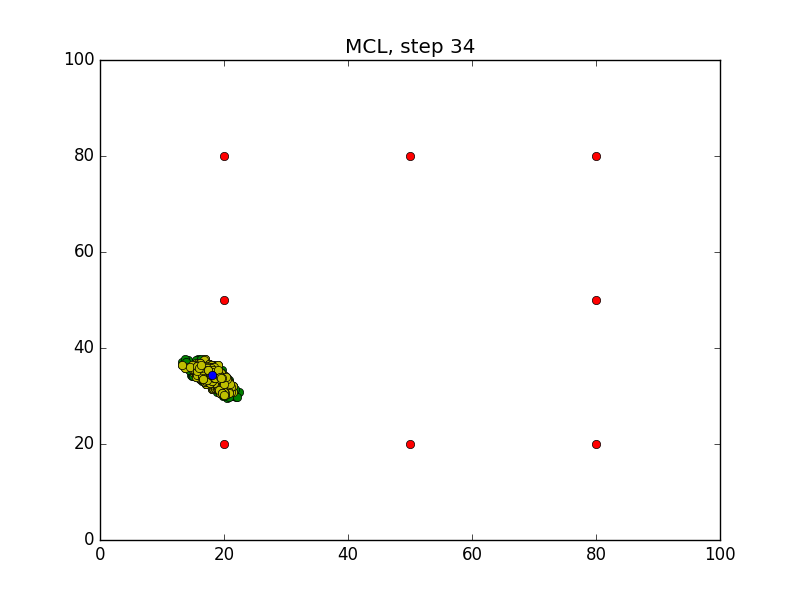Iteration 34 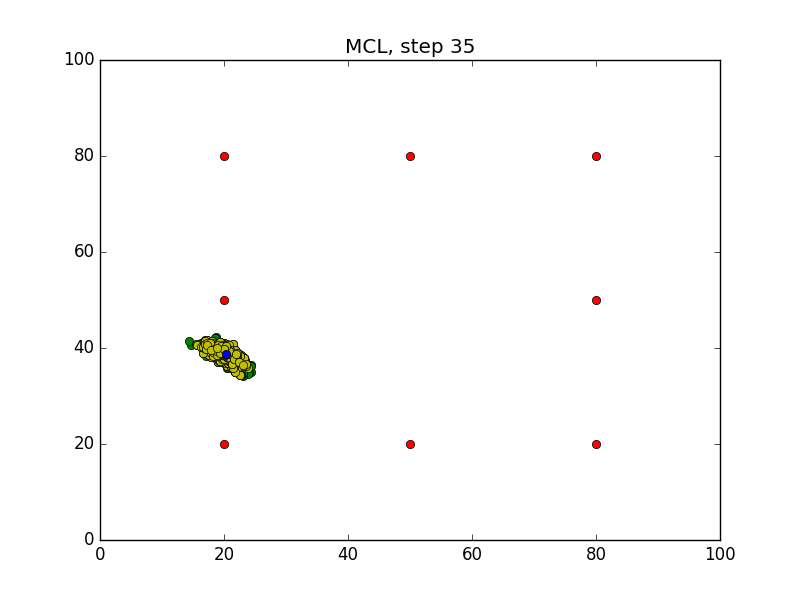Iteration 35 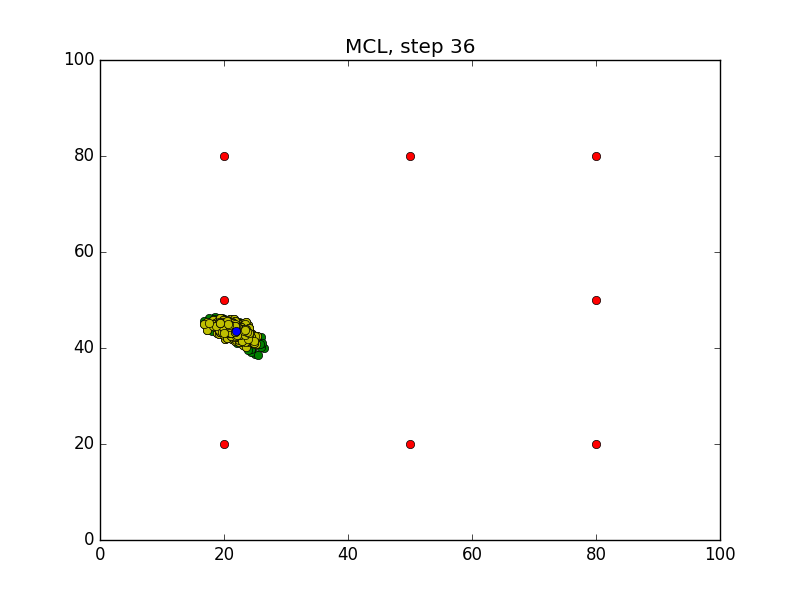Iteration 36 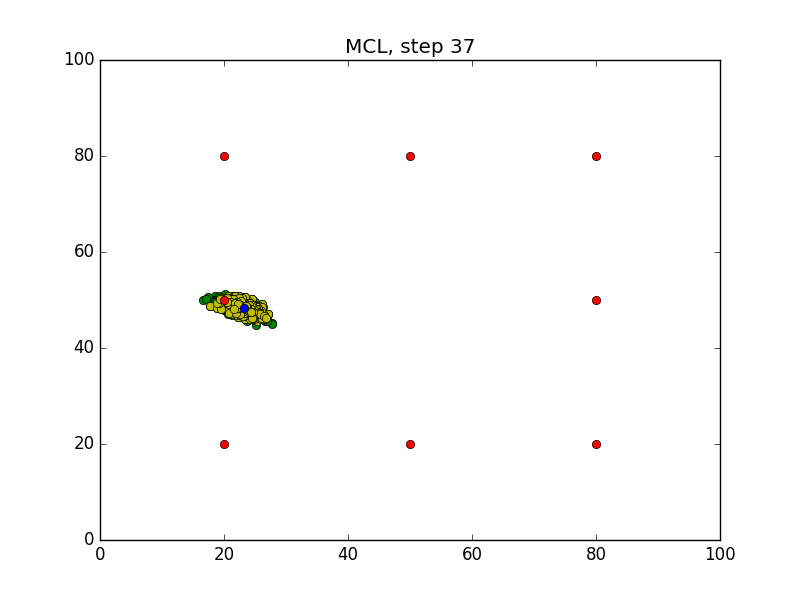Iteration 37 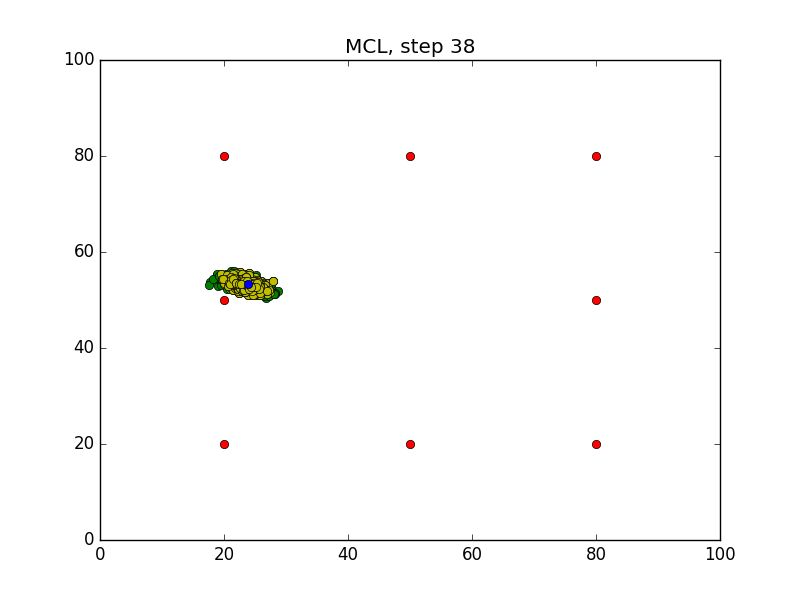Iteration 38 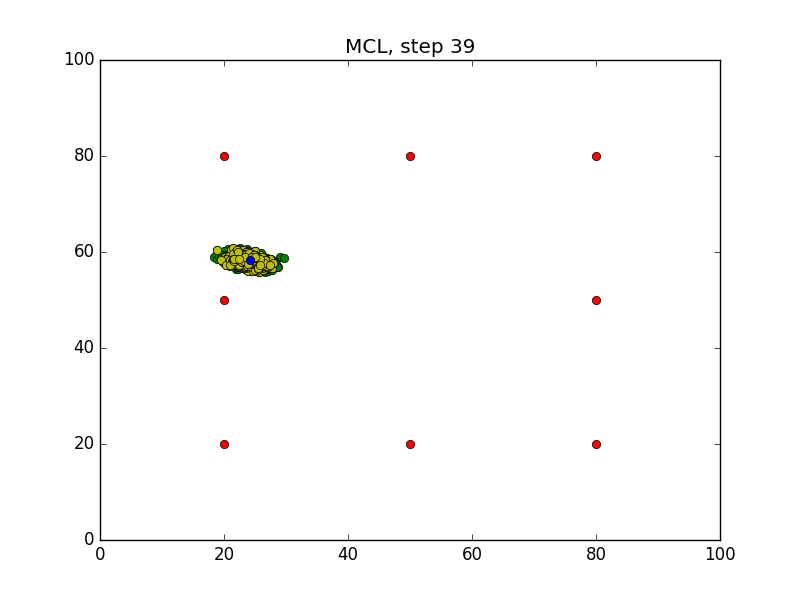Iteration 39
Iterations of the Monte Carlo Localization Algorithm.

Further details about MCL are found in the paper of Sebastian Thrun et al.

Reference

This post is a summary of the MCLLab from the Robotics Nanodegree of Udacity

Comments

You May Also Enjoy

Vector Robot

2 minute read

Regaining access to Vector Robot and working with the Vector Python SDK.

Vim Setup and Basics

1 minute read

Describes how to setup vim using a popular vimrc and explains the basics.